Building a Hagerman Inverse RIAA
Another page started ahead of schedule so it is not as complete as I'd like.


An Inverse RIAA is nice for debugging and burning in a phono preamp. You can buy a good Inverse RIAA from from Jim Hagerman like the one he detailed in his article on inverse RIAAs at his web site  Hagerman Technology LLC.  Unless you are a glutton for punishment, buy one from him. I needed a project to distract me while relatives were visiting over the holidays so I tossed this together.

The end result looks like this (yellow hand lettering on a purple painted box). The bottom has felt feet on it to keep from scratching table tops:

I added an electrostatic shield inside the box to help keep the channel cross talk down. In the picture below, the signal inputs are on the bottom. The insides with a brass electrostatic shield between channels looks like this:

I used two resistors to make the 41.66K.
I used three resistors to make the 513K. I could have gotten by with two resistors, but with three I could use what I had on hand.
I found a single 1.80 nF NPO cap that measured 1.79 nF
It took three NPO capacitors to get a 6.20 nF to within 1%.

I ran a brass divider between the two channels. The brass is bent on top and bottom so it presses against the top and bottom of the aluminum box.

I put it in a Philmore 1590BB Diecast aluminum box (4.68 x3.68 x1.33 $7.89 from Fry's electronics).

The first step is to prepare the box.
1. Sand the inside,
2. Screw the lid on, file the burrs off and then sand the outside.
3. Drill the 1/4 holes for the RCAs (0.75 inch from edge of  box and 0.75 inch apart.)

Since I sanded the scale off the inside of the aluminum box and used internal tooth lock washers under the RCA nuts, I decided not to tie the grounds together with a wire.

I did not make an effort to set the gain to exactly -40.0000000 dB. -39.xx dB was good enough.


How Accurate is it?

First a discussion of errors in dB. An error of 0.1 dB (+1.16%) is really pretty tight. Don't over react to the values you see in the plots. If we consider a circuit where the gain is 100% proportional to the resistor value, we end up with a table that looks like this:
 
RESISTOR
VALUE		 PERCENT ERROR IN 
RESISTOR VALUE		 ERROR 
IN DB
613200 20.00% 1.584
562100 10.00% 0.828
536550 5.00% 0.424
521220 2.00% 0.172
516110 1.00% 0.086
513555 0.50% 0.043
511511 0.10% 0.009
511000 0.00% 0.000
510489 -0.10% -0.009
508445 -0.50% -0.044
505890 -1.00% -0.087
500780 -2.00% -0.175
485450 -5.00% -0.446
459900 -10.00% -0.915
408800 -20.00% -1.938


Lets start with repeating the work of Jim Hagerman and show the Lipshitz, stock Hagerman and a tweaked Hagerman Inverse RIAA.

When I sent a pre-release of this page to Jim for comment**, Jim was nice enough to tell me that R4 in the schematic below is not 353.3 ohms (the value used in his article) but actually 332.42 ohms. It doesn't make too much of a difference in the audio band, but a mathematical reference is a reference that does not cost anything to have a few extra places accuracy.

I originally tweaked the circuit up with R4 = 353.3 ohms and came up with R18 = 1.3K. With R4 equal to 332.42 ohms, R18 looks better at 1.18K (A 12.7k across the 1.3K)

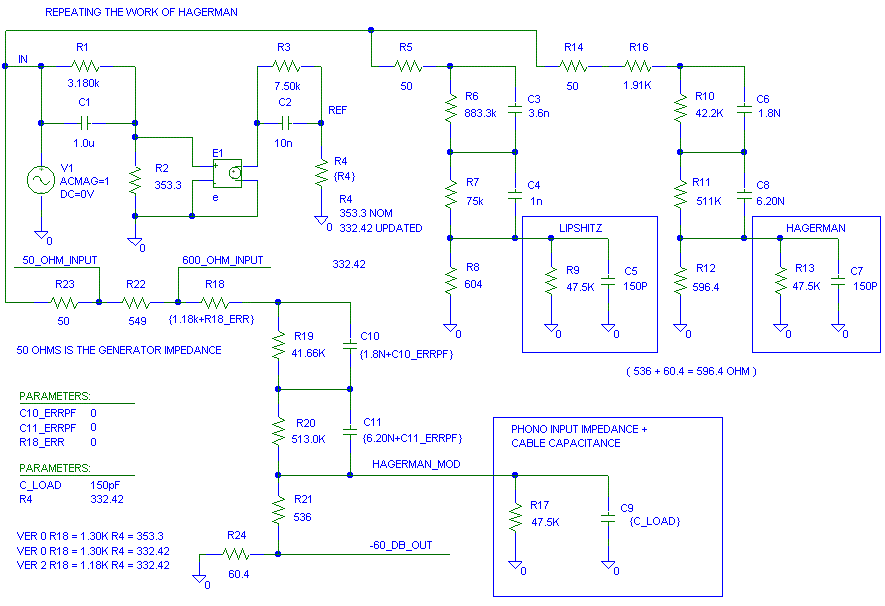
Here are the errors in dB of the three circuits versus the ideal response. Hagerman's design actually is good to start with. As you will find out in a minute or two, +/- 0.07 dB variation is nothing compared to what the part value differences will do. In the graph below I changed R4 from 353.3 ohms to 332.42 per Jim's comments (thanks) and left R18 = 1.30K (what worked best with 353 ohms). It is still not too bad.

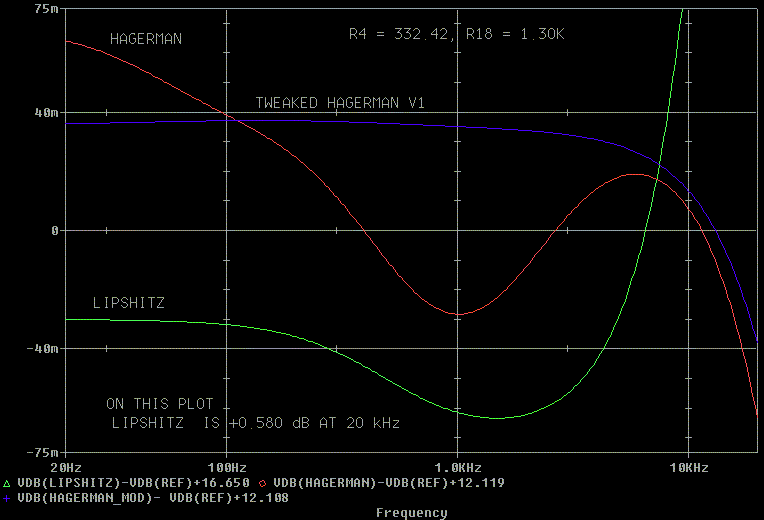
I played just a little with R18 and changed it from 1.3K to 1.18K and got slightly better results.

Since we can measure resistors with an ohm meter, we can trim the resistor values to be as accurate as we want or as accurate as our ohm meter.
I can get 41.66K by using a 51.1K in parallel with a 226K.
The 513K can be a 511K with a series 2K. (I used three resistors to get 513K because I didn't have a 511K on hand.)

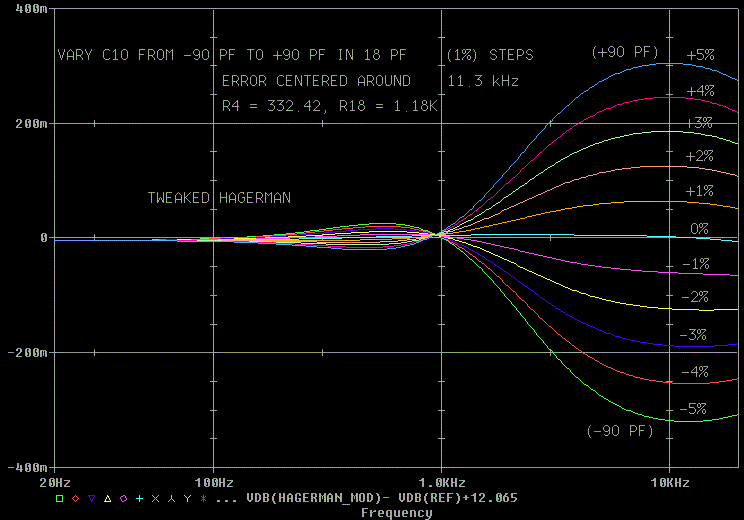
Since the resistors can be set much better than 1% manually, lets wiggle the 1800 pF (C10) capacitor values between -5% and +5% in 1% steps (18 pF) and see what happens.
Note the change in scale from +/- 0.075 dB to +/- 0.400 dB. Look how much more the capacitor variation is than the variation of the "ideal" circuit (0%.)

Now lets wiggle C11. Notice how C11 (6200 pF) changes the level everywhere. C10 (1800 pF) changes mostly just at 11 kHz.

I don't see the point in trimming the capacitors. If you want to try, here is what I'd do:
First start by setting the 170.6 Hz gain to be 3.373 times the DC output level.
Then try to set the 11.22 kHz gain to be 52.458 times the DC output level.
Measure the gain, convert to dB (20 log (V1/ V2)), look it up on the chart and correct the value.
Note: The 20 Hz level is 1.0761 times the DC level.

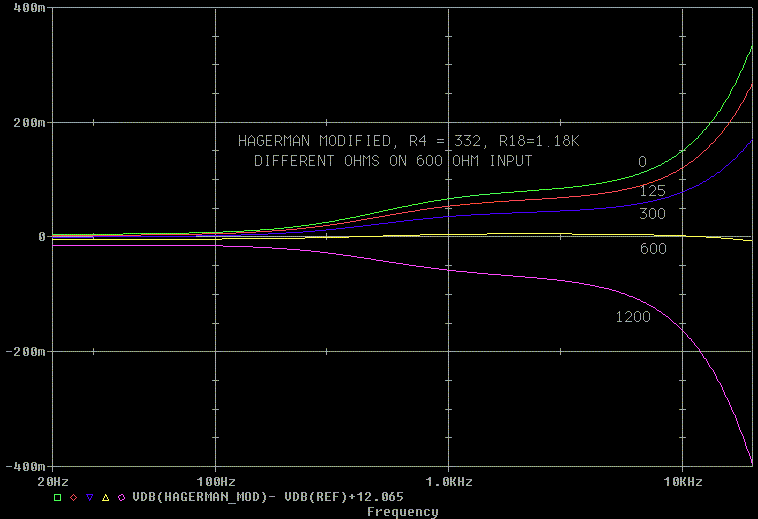
Now lets take a look at what happens if the input resistance from the generator is wrong.
Boy, everything moves if we use a microscope and we hit the table with a hammer. But we don't listen with a microscope.


**If I quote somebody's web site, I usually send them notice that I am quoting them. Jim was kind enough to send me the note about the R4 change. So I updated my site.

First edition 24-Dec-02, Last Update 7-Apr-2003
I don't change the update date on individual sections for minor corrections. I only change the date  for content changes.