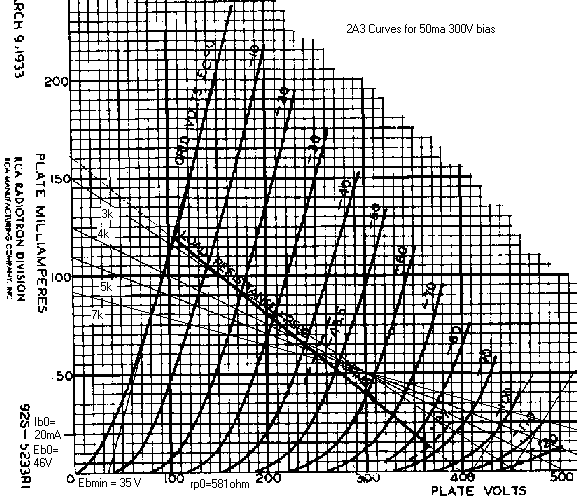
Figure 1: 2A3 curves with several load lines,
300V 50 mA bias point.
(Look at the thinly drawn load lines only.)
When using a graphical approach as in RDH equations (23) and (30) below, the optimum load line (RL opt) is where the tube runs out of voltage swing and current swing at the same time. This should be maximum output power for the tube at this bias point. Any other point will have either less current available or less voltage available. Both less current and less voltage means less output power.
Is maximum output power the best choice for RL? I depends. Maximum output power doesn't guarantee best damping factor or best distortion. When we get to the Pspice load line checks (not done yet), we may be able to tell more. Also, keep in mind while you are working the numbers that it is definitely not worth fighting for 10% (0.41 dB) more output power.
As a rule in class A single ended tubes, the peak to peak current into load cannot exceed twice the bias current.
* At one end of the load line, the tube
is conducting zero current and the plate choke or plate CCS is providing
100% of the bias current into the load.
* At the other end of the load line, the
tube is conducting twice the bias current: half of the current is driving
the load, half of the current is driving the plate choke or plate CCS.
If you use a load line lower in impedance than optimum, the tube will run out of current early. (With the same bias point optimized for 2k5, a 1k25 load line will run out of current swing before a 2k5 load line will.)My gut feel is it is usually better to run out of voltage before you run out of current. In a later edition of this web page I'll explain why (in lots of detail.) The heart of the "higher being better" matter is speakers and output transformers have dips in their impedance. So if you design the load line a little high, the tube is less likely to have trouble with the load. But you can make things too high and have parasitics eat your cake and sonics too! ;-)If you use a load line higher in impedance than optimum, the tube will run out of voltage early. (With the same bias point optimized for 2k5, a 5k0 load line will run out of voltage swing before a 2k5 load line will.)
If the load line is off by 20% from optimum
or 20% from what you want,
don't worry about it!
Do you really think your speakers are exactly 8 ohms?
Figure 1: 2A3 curves with several load lines,
300V 50 mA bias point.
(Look at the thinly drawn load lines only.)

Ib1 = current at the bias point.
Eb1 = voltage at the bias point
rp0 = plate resistance with zero volts on the grid. Pick two points on the straight line portion of the zero grid volt curve and calculate
rp0 = (V_high - V_low ) / (I_high -
I_low )
For a 2A3 I get 581 ohms.
I took many points and averaged them to get 581 ohms because I was doing this calculation for a web page. Doing the calculations by hand I came up with 600 ohms. 600 ohms would have been good enough. Remember, rp0 is not the same as rp specified in the tube manual for the tube. The spreadsheet linked to below actually does a curve fit to determine rp0 and comes up with still a different answer for the value of rp0.Ebmin = Voltage with zero volts on the grid where the straight line approximation for rp0 intersects with zero plate current. I get 35V.It is a very good idea to "measure twice and cut once." However tube, load and transformer parameters do move around so we are actually "cutting with and ax": so don't sharpen your pencil too sharp when you "measure" draw the "cut line."Always pick the data points to determine rp0 with a current level greater than Ib1. The portion of the curve we are trying to fit will always have more current than Ib1.
Ib0 = current from tube curves where the tube slope starts to bend unacceptably at the maximum peak plate volts you will be using.
I drew a pair 581 rp lines on the 2A3 curves to help visualize the amount of distortion going on near 450V at low current. To me, Ib0 looks like 20 mA.Eb0 = Voltage with zero volts on the grid where the straight line approximation for rp0 intersects with Ib0. This can be calculated from
Eb0 = Ebmin + Ib0 * rp0
I get 46 V for 20 mA.
Optimum load lines are found by making a triangles out of the plate curves and calculating the length and slopes of the three sides. This is easiest to do by moving the bottom left corner to be zero volts and zero amps and then adding the offsets to do this back into the final answer.
1. The height of the triangle is the peak to peak load current swing: 2 *( Ib1 - Ib0). The height of the triangle in amps is not always the same as the current at the peak of the triangle. This is because the base of the triangle is at Ib0, not at 0 mA. The height of the triangle is the peak current - Ib0.
2. The bottom left corner of the triangle is at Ib0 and Eb0. Remember Eb0 = Ebmin + Ib0 * rp0.
3. The base of the triangle is at Ib0 and has no slope.
4. The top left side of the triangle is plate curve for zero bias on the grid. The slope of the line is equal to 1/ rp0. This line hits the x-axis of this triangle (0 mA plate) at Ebmin. (Slope is change in y divided by the change in x, or slope = change in I/ change in V or slope = 1/ resistance. )
5. The top right side of the triangle is plate curve for the desired load resistance. The slope equals -1/ Rl and passes through both the peak of the triangle and the bias point Eb1, Ib1.
6. With this information we now calculate the peak of the triangle:
I_pk = Ib1 + zero to peak load swing = Ib1 + ( Ib1- Ib0)7. Since the load line goes from the peak of the triangle through the bias point with a slope of -1/ Rl, we can calculate Rl (Plate Load Resistance):
V = Eb0 the bottom left corner of the triangle + 2 * ( Ib1- Ib0) * rp0 for the peak
to peak AC swing times the slope of the left side of the triangle.
V = (Ebmin + Ib0 * rp0) + 2 * ( Ib1- Ib0) * rp0 (substituting in Ebmin for Eb0)
V = Ebmin + ( Ib0 + 2 * (Ib1- Ib0) ) * rp0
-Rl = [Voltage at triangle's peak - Voltage at bias point] /
[ Current at triangle's peak - Current at bias point]
-Rl = [ Ebmin + ( Ib0 + 2 * (Ib1- Ib0) ) * rp0 - Eb1 ] /[ Ib1 + (Ib1- Ib0) - Ib1 ]
+Rl = [- Ebmin - ( Ib0 + 2 * (Ib1- Ib0) ) * rp0 + Eb1 ] /[ Ib1- Ib0 ]
+Rl = [Eb1 - Ebmin - Ib1 * rp0 - 2 * (Ib1- Ib0) ) * rp0 ] /[ Ib1- Ib0 ]
+Rl = [Eb1 - Ebmin]/[ Ib1- Ib0 ] - [ Ib1 * rp0] / [ Ib1- Ib0] - 2 * rp0
+Rl = (Eb1 - Ebmin - Ib0 * rp0) /( Ib1 - Ib0) - 2 * rp0 <-- which I'll call equation 30 VSa
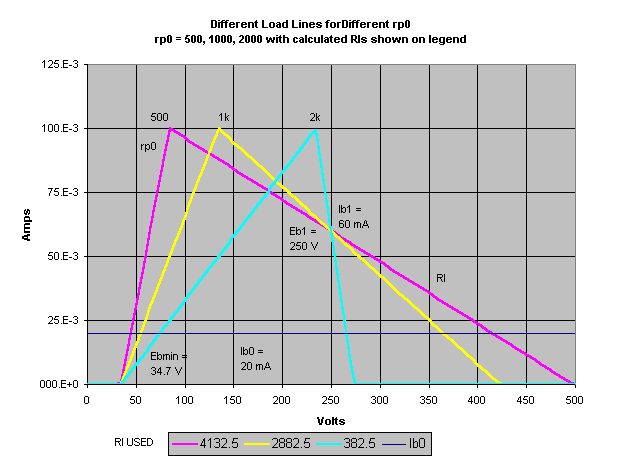
The tube current will swing from the peak current
to Ib0 on each set of load lines.
Notice how the load lines pivot around the bias
point and the peak current is always the same.
Also notice how the current swing from the "bias
point to the peak current" and the "bias point to Ib0" is the same in magnitude.
Table Chart 1: Output Power Levels for Chart 1.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I'm looking at chapter 13 of the RDH on biasing ideal triodes. For an ideal triode the best plate load is given by equation 23:
(23) Rl = (Eb1/ Ib1) - 2 * rp
Since rp changes with bias current, I'm changing this slightly to be:
(23 VS) Rl = (Eb1/ Ib1) - 2 * rp0
Formula (23 VS) matches the graphs in RDH which explain the bias curves he draws.
With a 2A3 with Pd = 15 W I can pick Ib1 = 50 mA and get Eb1 = 15W/ Ib1 = 300 V and rp0 = 581. Plugging these numbers into equation (23 VS) I get Example (23 VS):
Rl opt = (300 V/ 50 mA) - 2 * 581 = 6000 - 1162 = 4838 ohmsIf we use rp = 800 ohms from data sheet we get Example (23):
Rl opt = (300 V/ 50 mA) - 2 * 800 = 6000 - 1600 = 4400 ohms
RDH gives equation (30) for the best load line with a known Ib0. This allows us to pick a load line that keeps the tube away from the highly distorted low current area of the tube.
(30) Rl = (4 * Ib1/ Ib0 - 1) * rp0 + Ebmin/ Ib0
I don't understand RDH's Equation (30), it just does not make sense to me.
If I for a 2A3 I pick Ib1 = 50 mA, Eb1 = 300, Ib0 = 20 mA, Ebmin = 35, Eb0 = 46 and rp0 = 581, I get Example (30a):
Rl opt = (4 * 50 mA/ 20 mA - 1) * 581 + 35V/ 20 mA = 5229 + 1750 = 6979 ohms.If I lower Ib0 to 15 mA, Eb0 = 43V (Ebmin stays at 35V) I get Example (30b):
Rl opt = (4 * 50 mA/ 15 mA - 1) * 581 + 35V/ 15 mA = 9102 + 2333 = 11,435 ohms.What really bugs me is that if I have an almost ideal tube, Ib0 = 1 mA and Ebmin = 1V I get Example (30c):
Rl opt = (4 * 50 mA/ 1 mA - 1) * 600 + 1V/ 1 mA = 119.4 k + 1 = 119.4 kohms.Example (30c) should have given be the same answer as Equation (23 VS) but it did not.
If I derive a new Eq. (30) and introduce Eb0, I get
(30 VS) Rl opt = (Eb1 - Eb0) / (Ib1 - Ib0) - 2 * rp0
or since Eb0 = Ebmin + Ib0 * rp0
(30 VS a) Rl opt = ( Eb1 - Ebmin - Ib0 * rp0 ) /( Ib1 - Ib0 ) - 2 * rp0
So for our example with Ib0 = 20 mA, Eb0 = 46 we have Example (30 VS b):
Rl opt = (300 V - 46 V)/(50 mA - 20 mA) - 2 * 581 = 8467 - 1162 = 7305 ohmsSo for our example with Ib0 = 15 mA, Eb0 = 43 we get Example (30 VS c):
Rl opt = (300 V - 43 V)/(50 mA - 15 mA) - 2 * 581 = 7343 - 1162 = 6180 ohmsIf I have an ideal tube, Ib0 = 0 mA and Eb0 = 0V we get Example (30 VS d):
Rl opt = (300 V - 0 V)/(50 mA - 0 mA) - 2 * 581 = 6000 - 1162 = 4838 ohmsThis matches equation (23) for the ideal tube. This means the equation (30 VS a) has a chance at being right.
We can take equation (30 VS) and rewrite it to solve for the bias point when we know the load impedance. When we do this, we have to remember to stay below the rated maximum static DC plate to cathode voltage.
First we plug Eb1 = Pd/ Ib1 into equation (30 VS)
Rl
= [( Pd/ Ib1 - Eb0) / (Ib1 - Ib0)] - 2 * rp0
Set Eb1 = Pd/ Ib1
Rl + 2 * rp0
= (Pd/ Ib1 - Eb0) / ( Ib1 - Ib0)
Add 2 * rp0 to both sides
Ib1 * (Rl + 2 * rp0) - Ib0 *
(Rl + 2 * rp0)
= Pd/ Ib1 - Eb0
Multiply by "Ib1 - Ib0"
0 = Pd/ Ib1 - Eb0
- Ib1 * (Rl + 2 * rp0) + Ib0 * (Rl + 2 * rp0)
Move left side to right side
0 = Pd + Ib1 *
[Ib0 * (Rl + 2 * rp0) - Eb0] - Ib1^2 * (Rl + 2 * rp0) Multiply by Ib1 and
collect terms.
0 = Ib1^2 * (Rl
+ 2 * rp0) - Ib1 * [Ib0 * (Rl + 2 * rp0) - Eb0] -Pd Multiply by -1
and rearrange terms.
Equation (50 VS)
We now use the quadratic equation to solve for Ib1:
X = [ -B +/- sqrt( B^2 - 4 * A * C)]/ ( 2 * A )
A = Rl + 2 * rp0
= 5000 + 2 * 581 = 6162
B = -Ib0 *( Rl
+ 2 * rp0) + Eb0 = -.020 * 6162 + 46 = -77.24
C = -Pd
= - 15
= -15
Ib1 = [77.24 +/- sqrt( 77.24^2
- 4 * 6162 *{ -15})] / (2 * 6162)
Ib1 = [77.24 +/- sqrt( 375686)]
/ (12,324) = 0.05600 and - 0.04347 Use the positive number.
Ib1 = 56.00 mA
Eb1 = Pd/ Ib1 = 15 W/ 56.00 mA = 265 V (268 V is less than 300 V so we are OK on voltage.)
Pout = 0.5 * Rl * (Ib1 - Ib0)^2
= 0.5 * 5000 * (56.00 mA - 20 mA)^2
Pout = 3.24 W to output transformer.
Note:
1. The maximum static DC plate to cathode voltage
for tube is a different measurement than the maximum voltage rating for
a BJT or FET.
The maximum voltage for a BJT and FET is the PEAK voltage where the part self destructs.2. Links to math sites to give you headaches or possibly prevent them..
The maximum voltage for a tube is the maximum static (no signal) bias voltage for the tube.
It is common for the plate voltage of a tube to go to twice the bias voltage without damaging tube (assuming the tube is in good shape.)
A graphical quadratic equation solver <-- Best so far3. We get a + and - answer out of the quadratic equation because Ib1 is squared in equation (50 VS). When you square a number, you loose the sign (the + or -) information (Meaning (-2)^2 = 4, (+2)^2 = 4). Both x^2 and x**2 mean to square x. The difference comes from what computer language you are using.
First of many quadratic equation solvers I found on web.
A third quadratic equation solver on the web.History of the quadratic equation
More math classes on the quadratic equation.
This is an easy question.
B+ = Vbias_plate-cathode + Vcathode-gnd + (I_bias - Ib0)*RL + Vsaturation_of_the_CCS.For example:
B+ = 300V plate-cathode + 50V_cathode-gnd + (50 mA - 10 mA) * 5K + 10VIf we assume -10% for the low AC line:
B+ = 560V minimum.
B+ = 560V / 0.90 = 622 V nominal B+.You do need to design the CCS to survive a tube arc thermally. If the CCS is overheated during a tube arc it will fail short. This destroys the CCS, kills the tube (you actually may have wanted to save that tube) and hopefully the fuse pops before the B+, cathode resistor and cathode bypass capacitor burns up.CCS loss nominal = (622 - 300 - 50)* 0.050A = 13.6 W
CCS loss tube shorted = (622 - 50V) * 0.050A = 28.6 W
This is an interesting question. To answer it, we have to put right corner of the plate to cathode bias triangle to be at
Vclip = B+ - voltage drop of the CCS - Voltage cathode to groundThis crosses 0 mA on the right at:
I = Ib0
V = Vclip - Ib0 * RlThe equation for the top right leg of the triangle is
I = (Vclip - V)/ Rl + Ib0The location of the left corner of the triangle is:
V = Eb0 = Ebmin + I * rp0The equation for the top left leg of the triangle is
I = Ib0
I = (V - Ebmin)/ rp0Setting the equations to be equal to find "V" which will be "Vpk" we get:
(V - Ebmin)/ rp0 = (Vclip - V)/ RL + Ib0So now we know what the peak voltage (Vpk) is. The bias point will be halfway between Vpk and Vclip.
V - Ebmin = (rp0/Rl) * (Vclip - V) + rp0*Ib0
V - Ebmin = (rp0/Rl)*Vclip - (rp0/Rl)*V + rp0*Ib0
V + (rp0/Rl)*V = (rp0/Rl)*Vclip + Ebmin + rp0*Ib0
V + (rp0/Rl)*V = (rp0/Rl)*Vclip + Eb0
V * (1 + (rp0/Rl)) = (rp0/Rl)*Vclip + Eb0
V * (1 + (rp0/Rl)) = (rp0/Rl)*Vclip + Eb0
V = Vpk = [(rp0/Rl)*Vclip + Eb0]/(1 + (rp0/Rl))
Vbias_CCS = 0.5 * {Vclip + Vpk)For example, lets say we have an existing 2A3 parafeed design that has a 360V B+ (at 50 mA), Vccs min = 10V and Vcath-gnd estimate = 50V. So Vclip = 300V, Rl = 5000 ohms, rp0 = 581, Ebmin = 35V and Ib0 = 10 mA.Vbias_CCS = 0.5 * {Vclip + [ Eb0 + (rp0/ Rl)* Vclip ]/(1 + rp0/Rl) }Vbias_CCS = 0.5 * {Eb0 + {1 + 2* (rp0/ Rl)}* Vclip ]/(1 + rp0/Rl) }
Vbias_CCS = 0.5 * {Vclip * (1 + rp0/Rl) + Eb0 + (rp0/ Rl)* Vclip ]/(1 + rp0/Rl) }
Vbias_CCS = 0.5 * {Eb0 + Vclip + (rp0/ Rl)* Vclip + (rp0/ Rl)* Vclip ]/(1 + rp0/Rl) }
Vbias_CCS = 0.5 * {Eb0 + Vclip + 2* (rp0/ Rl)* Vclip ]/(1 + rp0/Rl) }
Vbias_CCS = 0.5 * {Eb0 + {1 + 2* (rp0/ Rl)}* Vclip ]/(1 + rp0/Rl) }Ibias_CCS = Ib0 + (Vclip - Vbias_CCS)/ Rl
Vclip = 360 - 10 - 50V = 300VWhen we look at the plate curves we see 184V, 33 mA takes about -33V grid-cathode so lets split the difference and use 41V Vcath-gnd and recalculate
rp0/Rl = 581/5000 = 0.1162
Eb0 = 35V + .010*581 = 40.81
Vbias = 0.5 * (40.81 + (1 + 2*.1162)*300V)/(1 + .1162) = 183.9V
Ibias_CCS = 10 mA + (300-183.9)/5000 = 33.2 mA
Pout = 0.5 * (300-183.9)^2/5000 = 1.35 Watts
Vbias = 189VIf we drop Ib0 to 5 mA
I_bias = 34 mA
Pout = 1.44 Watts (0.28 dB different, don't worry about it)
Vclip
= 309V
Eb0
= 37.91V
Vbias
= 187.5V
I_bias
= 29.8mA
Pout
= 1.47 Watts
The good news is if we lower the Ibias_CCS to 29.8 mA, B+ will rise and we can pick up a bit more voltage swing.
In RDH chapter 13, equation 7b, the second harmonic distortion of a triode is given by:
H2 = 100% * ( AQ/QB - 1) / [ 2 * ( AQ/QB + 1) ]
Q is the voltage on the plate with zero AC on the grid.
A is the voltage on the plate at the positive peak of the grid AC voltage (usually done with the grid to cathode at 0V )
B is the voltage on the plate at the negative peak of the grid AC voltage (usually done with the grid to cathode at twice the grid to cathode bias voltage)AQ is the voltage at A minus the voltage at Q
QB is the voltage at Q minus the voltage at BDF = Rl (primary side)/ (rp + total reflected primary DCR) = damping factor
So using the load lines in Figure 1 we get:
Table 1: Graphical Load Analysis from 2A3 Tube Curves at a 300V 50 mA Bias Point
|
|
|
|
|
|
|
|
|
|
rp0 = 581 |
|
|
|
|
|
|
|
used |
Volts ( 0 V grid ) |
Volts ( Bias point ) |
Volts ( 2x bias V) |
|
|
|
|
|
|
1 dB Xfmr loss |
|
|
Typ rp |
with 1 dB Xfmr loss |
with 0.5 dB Xfmr loss |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
One thing we see from Table 1 is that if we want to keep the better damping factors with high ohm Rls, we need transformers with lots of copper for the amount of gauss they swing. Most of the time a 0.5 to 1.0 dB insertion loss will be fine. If the DCR of the primary of a parafeed transformer is about 1/2 the rp, you will typically halve the best available damping factor from that tube and Rl combination. This usually is acceptable.
The "Watts out" do not include any losses in the
output transformer or speaker cables.
Typically expect to lose 5 - 15% of your output
power in the output transformer and cabling.
Table 2: Bias Points vs 20 mA Ib0 [very low distortion allowed)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Table 3: Bias Points vs 15 mA Ib0 [Kind of low distortion allowed]
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Table 4: Bias Points vs 10 mA Ib0 [moderate distortion allowed]
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Table 5: Bias Points vs 0 mA Ib0 [higher distortion allowed]
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Lets look at a couple bias points with different Ib0 and rp0. To calculate a 2A3's damping factor, I think rp = 1000 ohms is more realistic than 581 or 800 ohms. The published rp for the 2A3 I checked was 800 ohms. They did not specify the bias conditions for this rp.
Note: The tables below uses rp0 to calculate the damping factor.
Table 6 Rl vs rp0 with Ib0 = 20 mA
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Now let's cut Ib0 in half.
Table 7 Rl vs rp0 with Ib0 = 10 mA
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Not let's use a perfect tube with Ib0 = 0 amps.
Table 8 Rl vs rp0 with Ib0 = 0 mA
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
That's a lot of numbers to look at! I hope you see the same things I do.
1. When calculating the best Rl, we need to use rp0 from the zero grid voltage not the published rp.Using a different Rl than optimum is similar to changing Ib0 and/or changing Ebmin.
2. When calculating the best Rl, we need to give Ib0 serious consideration.
3. When calculating the best Rl, we still don't know how it sounds.
Raising Ebmin keeps you away from grid conduction.
Raising Ib0 keeps you away from low current tube nonlinearities.
Duncan Amps has Pspice models for tubes (click here for link.) With these models you can do detailed analysis on the circuit with out burning your finger even once on the soldering iron. Like all models, they "under describe the world" (a Mike LaFevre quote.) However, on a good model, you'll usually get more variation from tube to tube that you will from the model to the actual circuit.
Pspice analysis of the effects of inductance on the load line. On this "effects of inductance on the load line" page, I go over what happens if you don't have enough primary inductance. To a decent extent, if you bias the tube so that the load line is acceptable for the parallel load combination of the primary inductance and the actual reflected speaker load at 20 Hz, the inductive distortion effects should be low enough. I picked 20 Hz for the bias frequency so that we'll have margin at 32 Hz, not so that we can play synthesized 20 Hz bass.
Here is a copy of figure 1 and right below it I plotted the curves from the 2A3 Pspice model. Don't look too close if you aren't versed in the issues with making electrical models. It looks worse than it really is.
Figure 1: 2A3 curves with several load lines,
300V 50 mA bias point.

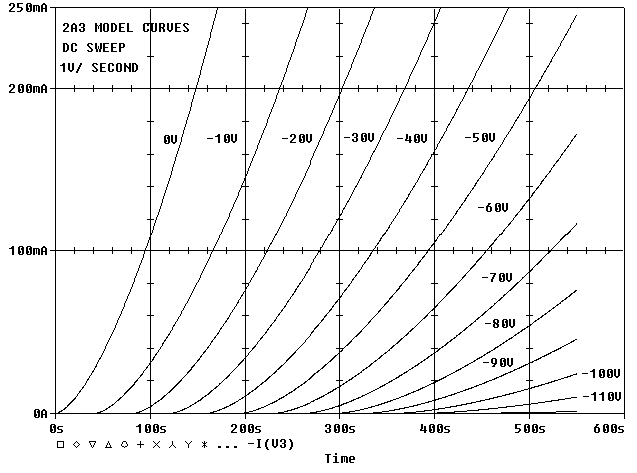
Are the curves identical? No. Are they good enough
to see trends? Yes. To me the PSPICE model looks like it has more gain
than the manufacture's graph. To compensate, I'll lower the grid voltages
to keep the bias point constant in the model. This will help keep the playing
field a bit more level.
 Power
Tube Load Lines Ver 2.11 (31-Dec-04)
Power
Tube Load Lines Ver 2.11 (31-Dec-04)
I put together a quick Excel SpreadSheet to do the calculations shown on this web page. Any polite suggestions you send me may be incorporated in to the spread sheet. Version 11 has several tube data points already loaded into it.
With the Excel file I discovered that if the equations spit out an RL less than rp0, the bias point numbers are wrong.
I also found that at a given voltage, if the bias current was more than 1/2 the bias current from the 0 V bias line, the optimum load current came out as negative.
This is really cool! It is a mystery to solve. I've probably going to have to do a bit more math to solve it.
More to come. . .